矩阵的QR分解

概述

$A=QR$这一过程将矩阵分解为$Q$和$R$两部分，其中$Q$是标准正交矩阵，$R$是一个上三角矩阵。

矩阵的$QR$分解能够简化计算可以以线性系统的计算为例，
$Ax=b\Longrightarrow (QR)x=b$
$Q^{-1}QRx=Q^{-1}b\Longrightarrow Rx=Q^Tb$
$Q^T$是非常好计算的，$R$是一个上三角矩阵（相当于Gauss-Jordan消元法的前向过程结束），从下往上推就可以很快计算出线性系统的结果。

因为涉及到求取标准正交矩阵$Q$的过程，所以矩阵$A$可以进行$QR$分解的条件是$A$的各个列向量是线性无关的。因为只有满足这一点才能进行Gram-Schmidt过程。

演示分析

$A=QR，其中A=(\vec{a_1},\vec{a_2},...,\vec{a_n})$
对矩阵$A$的各列执行Gram-Schmidt过程，得到正交向量$\vec{p_1}，\vec{p_2}，...，\vec{p_n}$，归一化后得到标准正交向量$\vec{q_1}，\vec{q_2}，...，\vec{q_n}$。
$\vec{p_1}=\vec{a_1}$
$\vec{p_2}=\vec{a_2}-\frac{\vec{a_2}\cdot \vec{p_1}}{||\vec{p_1}||^2}\cdot\vec{p_1}$
得到上三角矩阵$R$的过程如下，以$A$矩阵前3个列向量为例，


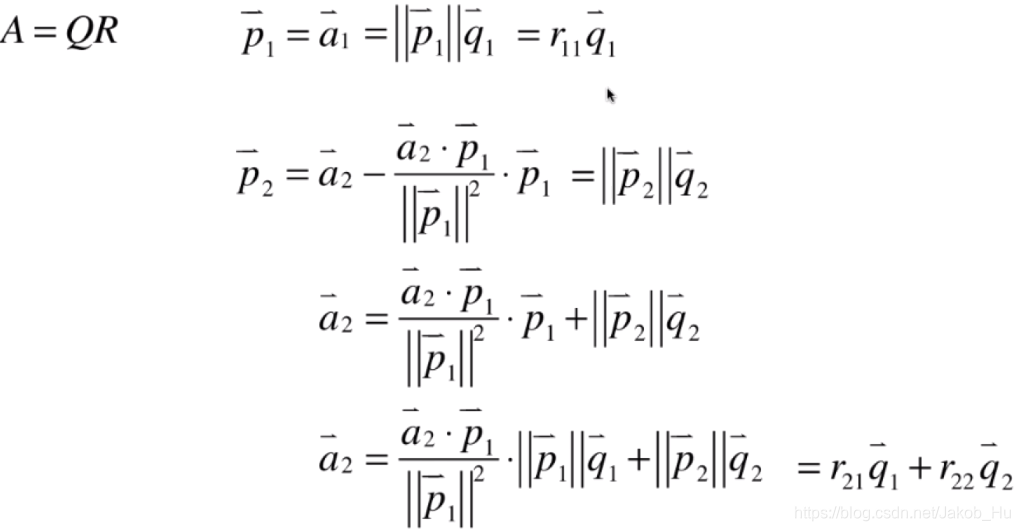
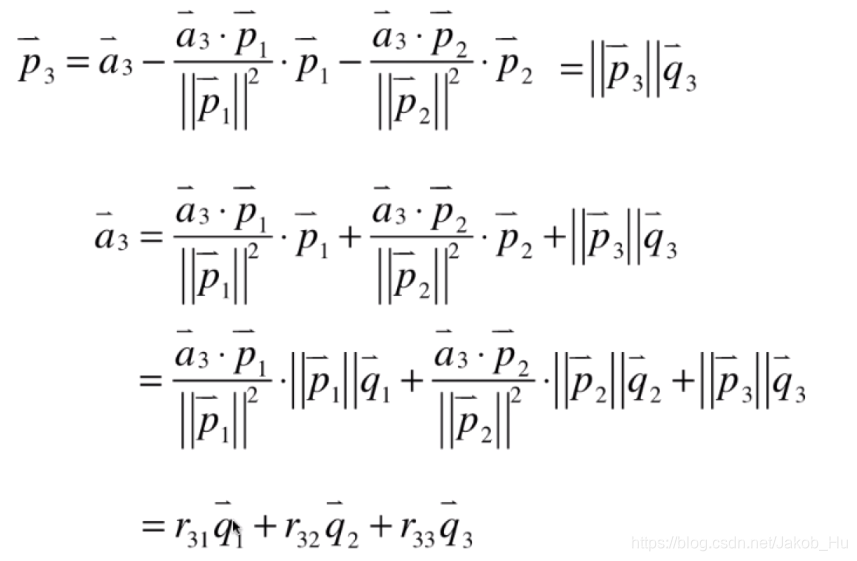
求取$R$的过程是使用已经求取的标准正交基反推原来的列向量。每一个系数都是可以找到规律的。故矩阵的$QR$分解实际上将矩阵A分解为如下形式，

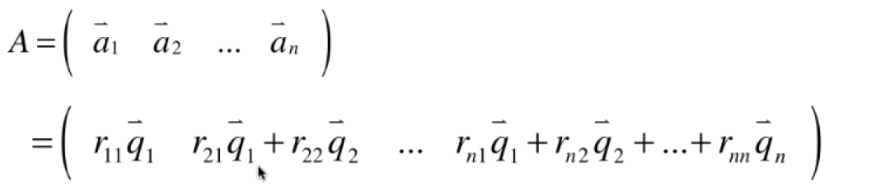
可以对该矩阵再进行推导，

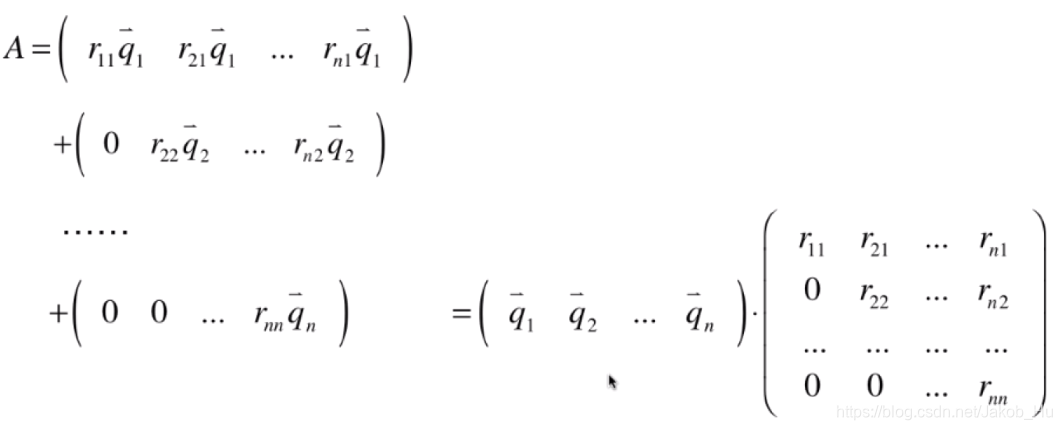
实现QR分解

上面的推导过程很复杂，但是在实际的计算过程中根本不需要求取$R$中的每个值，而是只需通过Gram-Schmidt过程得到$A$的标准正交矩阵$Q$，很快速的求取出$R$，通过如下形式，
$A=QR\Longrightarrow Q^{-1}A=R$
由正交矩阵性质可得，
$R=Q^{-1}A\Longrightarrow R=Q^TA$

def qr(A):
    """
    :param A: 一个矩阵对象，本节A是方阵，实际上一般矩阵也可以QR分解，只是本次不涉及
    """
    assert A.row_num() == A.col_num(), "A must be square"
    
    basis = [A.col_vector(i) for i in range(A.col_num())]
    P = gram_schmidt_process(basis)
    # 这里转置是因为在自定义的Matrix类中，是通过行向量创建矩阵的
    Q = Matrix([v/v.norm() for v in P]).T()    
    R = Q.T.dot(A)

    return Q, R


if __name__ == "__main__":
    A = Matrix([[1, 1, 2], [1, 1, 0], [1, 0, 0]])
    Q, R = qr(A)
    print(Q.dot(R))
    
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20