
荐二次抑制载波振幅调制接收系统 Python
发布于2020-03-20 13:45 阅读(1362) 评论(0) 点赞(11) 收藏(2)
快速链接:
二次抑制载波振幅调制接收系统
-
已知:
输入信号:
f(t)=sin(t)πt=Sa(t)π,−∞<t<∞ f(t)=πtsin(t)=πSa(t),−∞<t<∞
调制信号:
s(t)=cos(500t),−∞<t<∞ s(t)=cos(500t),−∞<t<∞ -
问: 输出信号
y(t)=? y(t)=?
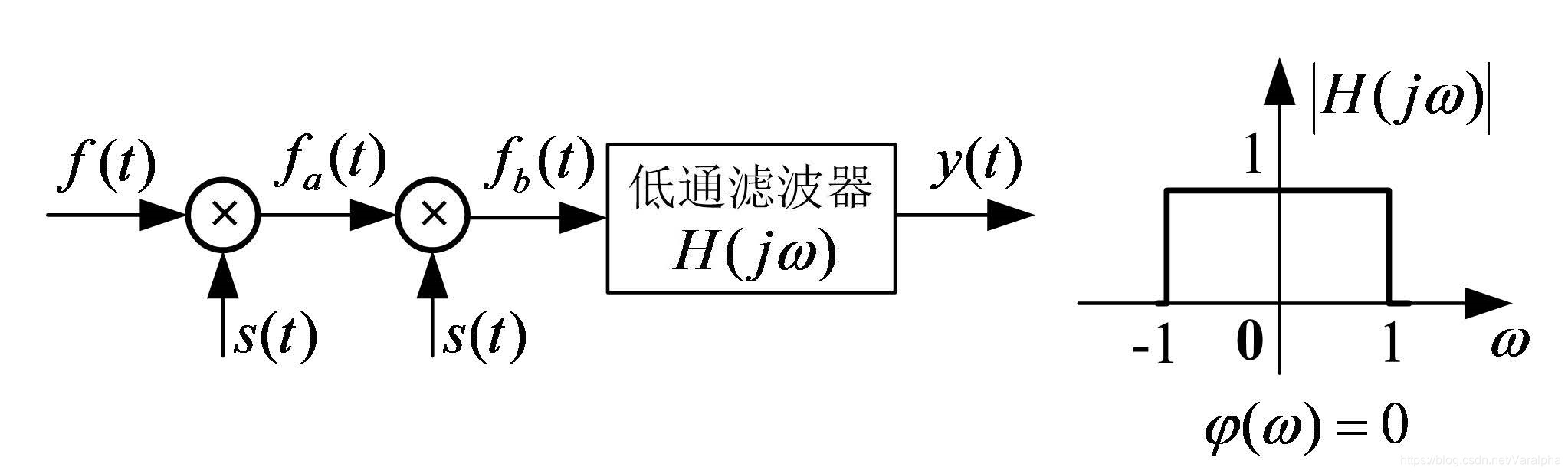
-
下式说明:
Sa(t)/π Sa(t)/π 为非周期, 使用 傅里叶变换分析法- 步骤 (详见):
- 从图中已知系统函数
H(jω)=g2 H(jω)=g2 门宽为2 2 ; - 求输入信号
f(t) f(t) 的傅里叶变换F(jω) F(jω) ; - 求调制信号的傅里叶变换
S(jω) S(jω) ; - 求零状态响应
y(t) y(t) 的傅里叶变换Y(jω)=Fb(jω)⋅H(jω) Y(jω)=Fb(jω)⋅H(jω) ; - 求
Y(jω) Y(jω) 的傅里叶逆变换y(t)=F−1[Fb(jω)H(jω)] y(t)=F−1[Fb(jω)H(jω)] 。
- 从图中已知系统函数
- 其中
δ δ 卷积特性δ(k−k1)⋆δ(k+k2)=δ(k−k1+k2) δ(k−k1)⋆δ(k+k2)=δ(k−k1+k2)g(ω) g(ω) 门函数特性 为0,ω>1orω<−1 0,ω>1orω<−1
-
可知
H(jω)=g2(ω) H(jω)=g2(ω)
f(t)=Sa(t)πs(t)=cos(500t)⟷g2(ω)=F(jω)⟷π[δ(ω+500)+δ(ω−500)]=S(jω) f(t)=πSa(t)s(t)=cos(500t)⟷g2(ω)=F(jω)⟷π[δ(ω+500)+δ(ω−500)]=S(jω)y(t)Y(jω)y(t)=f(t)×s(t)×s(t)⋆h(t)=14π2F(jω)⋆S(jω)⋆S(jω)⋅H(jω)=14π2g2(ω)⋆π[δ(ω+500)+δ(ω−500)]⋆π[δ(ω+500)+δ(ω−500)]⋅H(jω)=14π2g2(ω)⋆π2[δ(ω+1000)+2δ+δ(ω−1000)]⋅H(jω)=14g2(ω)⋆[δ(ω+1000)+2δ+δ(ω−1000)]⋅g2(ω)=12g2(ω)=Sa(t)2π=12f(t) y(t)Y(jω)y(t)=f(t)×s(t)×s(t)⋆h(t)=4π21F(jω)⋆S(jω)⋆S(jω)⋅H(jω)=4π21g2(ω)⋆π[δ(ω+500)+δ(ω−500)]⋆π[δ(ω+500)+δ(ω−500)]⋅H(jω)=4π21g2(ω)⋆π2[δ(ω+1000)+2δ+δ(ω−1000)]⋅H(jω)=41g2(ω)⋆[δ(ω+1000)+2δ+δ(ω−1000)]⋅g2(ω)=21g2(ω)=2πSa(t)=21f(t)
# 导入 需要的 library 库
import numpy as np # 科学计算
import matplotlib.pyplot as plt # 画图工具
import scipy.signal as sg # 导入 scipy 的 signal 库 重命名为 sg
# 用 Python 表示
t = np.linspace(-4*np.pi,4*np.pi,1601)
def draw_graph(t,f,title): # 设置好绘图参数
plt.plot(t,f,'-')
plt.xticks(t[::200],[fr'${int(i/np.pi)}\pi$'for i in t[::200]])
plt.title(title)
plt.grid(True)
plt.show()
ft = np.sin(t)/(np.pi*t)
# 开始绘图
draw_graph(t,ft,r'$f(t)$')

st = np.cos(500*t)
fat = ft*st
# 开始绘图
draw_graph(t,fat,r'$f_a(t)$')

fbt = fat*st
# 开始绘图
draw_graph(t,fbt,r'$f_b(t)$')
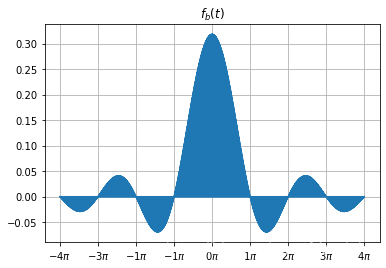
ht = np.sin(t)/(t*np.pi)
yt = sg.convolve(fbt,ht)*(np.pi/200) # 低通滤波器
draw_graph(t,yt[800:2401],r'$y(t)$')
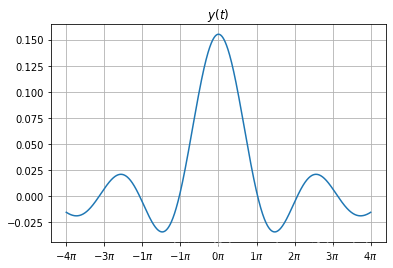
- 为更清楚展示原理, 取
s(t)=cos(10t) s(t)=cos(10t)
st = np.cos(10*t)
fat2 = ft*st
# 开始绘图
draw_graph(t,fat2,r'$f_a(t),\; s(t) =\cos(10t)$')

fbt2 = fat2*st
# 开始绘图
draw_graph(t,fbt2,r'$f_b(t),\; s(t) =\cos(10t)$')
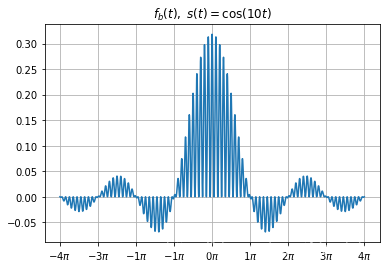
yt2 = sg.convolve(fbt2,ht)*(np.pi/200)
# 开始绘图
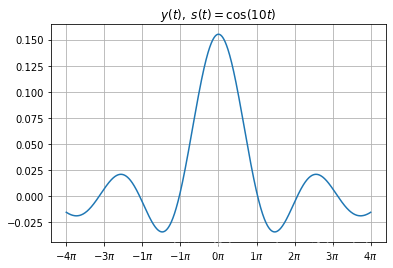
draw_graph(t,yt2[800:2401],r'$y(t),\; s(t) =\cos(10t)$')
所属网站分类: 技术文章 > 博客
作者:战天
链接:https://www.pythonheidong.com/blog/article/271237/b3fa030140a14b61c53c/
来源:python黑洞网
任何形式的转载都请注明出处,如有侵权 一经发现 必将追究其法律责任
昵称:
评论内容:(最多支持255个字符)
---无人问津也好,技不如人也罢,你都要试着安静下来,去做自己该做的事,而不是让内心的烦躁、焦虑,坏掉你本来就不多的热情和定力